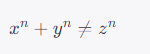L’affascinante storia dei numeri primi, mai in solitudine

I numeri primi hanno una storia lunga e affascinante che attraversa molte culture e epoche. Un numero primo è un numero naturale maggiore di 1 che non ha divisori positivi oltre a 1 e se stesso. I primi esempi di numeri primi sono 2, 3, 5, 7 e 11.

Antichità

• Gli Antichi Greci: La teoria dei numeri, e in particolare quella dei numeri primi, ha le sue radici nell’antica Grecia. Euclide, nel suo “Elementi” (circa 300 a.C.), dimostrò che esistono infiniti numeri primi.
• Eratostene: Un altro matematico greco, Eratostene, ha creato un algoritmo per trovare numeri primi chiamato “Criba di Eratostene”.

Medioevo e Rinascimento

• Medioevo: Durante il Medioevo, i matematici come Fibonacci portarono nuove idee e conoscenze nel mondo occidentale, inclusa una maggiore comprensione dei numeri primi.
• Pierre de Fermat: Fermat, nel XVII secolo, formulò il piccolo teorema di Fermat e congetturò il teorema degli ultimi Fermat, che rimase irrisolto fino al XX secolo.

Età Moderna

• Carl Friedrich Gauss: Gauss, nel XIX secolo, ha profondamente influenzato la teoria dei numeri e studiò le proprietà distributive dei numeri primi, formulando la legge della reciprocità quadratica e congetture riguardanti la distribuzione dei numeri primi.
• Bernhard Riemann: Riemann ipotizzò nel 1859 l’ipotesi di Riemann, che riguarda la distribuzione degli zeri della funzione zeta di Riemann e che è strettamente collegata alla distribuzione dei numeri primi. L’ipotesi di Riemann rimane uno dei più grandi misteri irrisolti della matematica.

XX e XXI Secolo

• Andrew Wiles: Nel 1994, il matematico britannico Andrew Wiles, con l’aiuto di Richard Taylor, riuscì a dimostrare il Teorema di Fermat, utilizzando tecniche avanzate dalla geometria algebrica e dalla teoria dei numeri.
• I Numeri Primi e la Crittografia: Nel tardo XX e nel XXI secolo, i numeri primi hanno trovato una nuova vita nella crittografia a chiave pubblica, come quella RSA, dove la fattorizzazione di grandi numeri è un problema computazionalmente difficile, garantendo la sicurezza dei dati trasmessi elettronicamente.

Premio per l’Ipotesi di Riemann

L’Ipotesi di Riemann è uno dei “Problemi del Millennio”, e chiunque riuscisse a dimostrarla (o a refutarla) riceverebbe il Premio del Millennio, che ammonta a un milione di dollari, offerto dal Clay Mathematics Institute.

Prima degli Antichi Greci, molte civiltà avevano una certa comprensione dei numeri primi e della matematica in generale, ma non è sempre chiaro quanto siano state approfondite le loro conoscenze nella teoria dei numeri.

Babilonesi

I Babilonesi erano noti per le loro capacità matematiche, e le tavolette cuneiformi dimostrano una sofisticata comprensione dell’aritmetica e dell’algebra. Tuttavia, non ci sono prove dirette che i Babilonesi studiassero i numeri primi per le loro proprietà intrinseche.

Egiziani

Gli antichi Egiziani avevano notevoli conoscenze matematiche, come dimostrato dal Papiro di Rhind, un documento che contiene molti problemi e soluzioni matematiche. Tuttavia, anche in questo caso, non ci sono indicazioni chiare che gli Egiziani studiassero i numeri primi in modo teorico, anche se erano sicuramente in grado di eseguire divisioni e fattorizzazioni.

Indiani Antichi

L’antica India aveva matematici che contribuivano in modo significativo allo sviluppo della matematica. I matematici indiani avevano una certa conoscenza della teoria dei numeri, e i numeri primi venivano utilizzati in alcuni contesti, ma ancora una volta, le prove dirette della teorizzazione sui numeri primi sono limitate.

La matematica nell’antica India, e in particolare nel contesto dei testi Veda, ha mostrato notevoli abilità e intuizioni in molte aree. I testi matematici indiani antichi, come i “Sulba Sutras”, che sono annesse a diversi Veda, includono varie regole e procedure per misurazioni, costruzioni geometriche, e altro. I matematici indiani avevano sviluppato sofisticate tecniche aritmetiche, algebraiche, e geometriche.

Nel contesto dei numeri primi, ci sono alcune indicazioni che i matematici indiani erano al corrente del concetto e utilizzavano i numeri primi in calcoli specifici. Ad esempio, nella “Aryabhatiya”, un’opera fondamentale dell’astronomo e matematico indiano Aryabhata (476-550 d.C.), vi sono dimostrazioni di conoscenze relative ai numeri primi e ai loro reciproci.

Tuttavia, mentre i matematici indiani antichi avevano una chiara comprensione dei numeri primi e li utilizzavano in vari contesti, non ci sono molte evidenze che suggeriscano un approfondimento teorico dei numeri primi analogo a quello sviluppatosi in seguito in Europa. Ciò non diminuisce in alcun modo i notevoli successi e contributi dei matematici indiani in varie aree della matematica.

È anche importante notare che la storia della matematica in India è ricca e complessa, e c’è ancora molto che gli studiosi stanno imparando riguardo alle profondità e all’ampiezza delle conoscenze matematiche nell’antica India.

Cinesi

La matematica cinese antica era altamente sviluppata e includeva conoscenze di aritmetica, algebra, e geometria. Sappiamo che erano capaci di risolvere equazioni algebriche e che utilizzavano un sistema decimale posizionale. Tuttavia, simile ad altre civiltà antiche, non abbiamo molte evidenze che suggeriscano uno studio approfondito dei numeri primi in Cina prima dell’influenza greca.

In generale, mentre le civiltà antiche utilizzavano i numeri primi e avevano alcune tecniche per identificarli e lavorarci (ad esempio, nella fattorizzazione), la teoria dei numeri in quanto tale sembra essere stata sviluppata in modo più sistemico dagli Antichi Greci, e molte delle idee e teorie più avanzate relative ai numeri primi emergono nel contesto della matematica greca e successivamente in quella europea.

Ma cos’è un numero primo?

Un numero primo è un numero intero positivo maggiore di 1 che ha esattamente due divisori positivi distinti: 1 e se stesso. In altre parole, un numero primo non può essere diviso esattamente (cioè, senza lasciare un resto) da nessun altro numero tranne 1 e se stesso.

Ecco alcuni esempi di numeri primi: $2,3,5,7,11,13,17,19,23,29,31,\dots$

Qui ci sono alcune proprietà chiave dei numeri primi:

• Unicità: Ogni numero naturale maggiore di 1 può essere scomposto in fattori primi in un modo che è unico a meno dell’ordine dei fattori. Questa è la cosiddetta “fondamentale teorema dell’aritmetica”.
• Infinità: Ci sono infiniti numeri primi. Questo fu dimostrato da Euclide più di 2000 anni fa.
• Distribuzione: Nonostante l’infinità dei numeri primi, non esiste una formula che generi tutti i numeri primi, e la loro distribuzione su grandi intervalli rimane oggetto di numerosi studi e congetture, come l’Ipotesi di Riemann.

I numeri primi hanno un ruolo centrale in numerosi campi della matematica e sono fondamentali per molte applicazioni pratiche, come la crittografia, grazie alle loro particolari proprietà e al fatto che la fattorizzazione di grandi numeri è un problema computazionalmente difficile.

Cosa dice il teorema di Fermat?

Pierre de Fermat, un matematico francese del XVII secolo, è noto per diversi teoremi e congetture nel campo della teoria dei numeri. Due delle sue affermazioni più note riguardano il Piccolo Teorema di Fermat e l’Ultimo Teorema di Fermat. Ecco una breve descrizione di entrambi:

Piccolo Teorema di Fermat

Il Piccolo Teorema di Fermat afferma che se $p$ è un numero primo e $a$ è un numero intero non divisibile per $p$, allora:

Ultimo Teorema di Fermat

L’Ultimo Teorema di Fermat è completamente diverso ed è stato famoso per essere un problema irrisolto per più di 350 anni. Fermat scrisse nel margine di un libro

per $n>2$ e $x,y,z$ numeri interi non nulli, affermando di avere una dimostrazione che però non ha mai scritto.

Questo enunciato è noto come l’Ultimo Teorema di Fermat poiché, tra le varie congetture e teoremi di Fermat, è stato l’ultimo a essere dimostrato. La dimostrazione è stata fornita da Andrew Wiles, con l’aiuto del suo allievo Richard Taylor, nel 1994, utilizzando tecniche avanzate di geometria algebrica e teoria dei numeri.

Entrambi questi teoremi hanno avuto un profondo impatto sulla matematica e hanno ispirato ulteriori ricerche nel campo della teoria dei numeri.